Бывшая учительница математики предложила решение задачи о трисекции угла

Ляля Зарипова. Фото: «Российская газета»

Вопреки вердикту

Одна из старейших математических загадок, доставшаяся человечеству от Архимеда, получила название задачи о трисекции угла. Древний мыслитель и один из отцов геометрии попытался разделить угол на три равные части с помощью циркуля и линейки. Однако найти решение не смог и завещал эту загадку ученикам и потомкам, сообщает «Российская газета».

Сегодня любой школьник легко разделит угол на две половины. Линейки и циркуля для этого вполне достаточно. Без особого труда можно разбить на три равные части прямой угол, встроив в него равносторонний треугольник. Однако разделить любой угол на три равные части ученые до сих пор не смогли.

Еще в 1736 году известный французский математик Пьер Ванцель, проигнорировав условия Архимеда о циркуле и линейке, попытался найти «трисекцию угла» алгебраическим путем и потерпел фиаско. В дальнейшем решение искать просто перестали. А в 1756-м Французская академия наук вынесла официальный вердикт о том, что эту задачу решить невозможно, и исключила ее из всех учебников и справочников того времени.

С тех пор о головоломке, некогда занимавшей лучшие математические умы, забыли. Бывшая учительница математики из Миасса Ляля Гиззатовна Зарипова искала «ключ» несколько лет и, перепробовав множество путей, нашла простое и блестящее решение, к которому, судя по оставшимся в истории записям, шел сам Архимед, но довести его до конца не сумел.

По мнению учительницы, чтобы разделить угол на три равные части, нужно провести из его основания окружность, отложить за ее пределами еще один радиус на биссектрисе, делящей этот угол пополам, и получить так называемый внешний угол. Он и будет в три раза меньше заданного угла, то есть станет одной из трех секций из условия задачи.

Отмечается, что последние три сотни лет решение даже не искали, а все это время математика шла семимильными шагами.

Автор геометрического подхода уверена: откладывая на биссектрисе нужное число радиусов, угол можно разделить не только на три, но и на пять, семь и девять частей — другими словами, разделить его на любое нечётное число. А это, в свою очередь, позволит найти решение еще одной математической головоломки — вписать в окружность любой правильный многоугольник. В справочниках до сих пор утверждается, что вписать правильные многоугольники, имеющие семь и девять сторон, в окружность невозможно.

Однако, прежде чем понять, что решение единственно верное, Ляле Гиззатовне нужно было найти для него теоретическое обоснование. Для этого она сформулировала и доказала три теоремы, подтверждающие правильность подхода. И только после этого поделилась с миром своим открытием. 

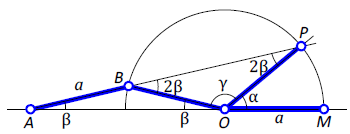Трисекция угла

Хождение по академиям

Однако, сетует Ляля Гиззатовна, рассказать о нем оказалось сложнее, чем сделать: «С января 2018 года звонила, писала, умоляя чиновников от науки об одном — выслушайте! Но наталкивалась на глухую стену непонимания. Письма нераспечатанными возвращали назад. В телефонных переговорах после слов о том, что мне удалось найти трисекцию угла, обещали перезвонить и не перезванивали. Вероятно, принимали за сумасшедшую. Ведь во всех учебниках написано, что решения у этой задачи нет»

Сначала учительница обратилась в Минобрнауки РФ, однако оттуда ее перенаправили в Российскую академию наук. В РАН сослались на реорганизацию и попросили написать в математический институт имени В.А. Стеклова, где объяснили, что занимаются высшей математикой, а вопросы, касающиеся элементарной математики, — компетенция специально созданного института по работе с научными открытиями.

«Директор этого учреждения, услышав голос «очередного изобретателя вечного двигателя», посоветовал получше изучить геометрию, в которой черным по белому записано, что задача о трисекции угла не имеет решения. А когда я начала его убеждать, посоветовал сначала опубликовать работу в каком-нибудь научном издании, а уж потом отнимать время у академиков», — вспоминает этот разговор учительница.

Дальше была переписка с Казанским и Новосибирским отделениями РАН, откуда Ляля Гиззатовна получила выдержку из Википедии. В итоге письмо учительницы вернулось обратно в Минобрнауки РФ.

Мнение учёных

Ляля Гиззатовна сняла ролик, в котором она делит угол на три равные части и предложила посмотреть его математикам из Челябинского государственного университета.

По мнению академика РАН Сергея Матвеева, этой проблемой занималось не одно поколение математиков: «Какое бы решение ни предложили, оно однозначно неверное. Иначе это действительно сенсация, и с ней можно претендовать на Нобелевскую премию».

«Мир остался прежним, как и его законы. Если вы бросите камень, он на Марс не улетит. Мы, конечно, можем посмотреть видео и, возможно, даже не обнаружим в этом решении ошибку, но она там обязательно есть. Мы бы посоветовали учительнице поискать ее самой», — цитирует газета доцента кафедры математики Филиппа Кораблёва.

Тем не менее математики потратили несколько минут на просмотр видео. Несмотря на высказанное недоверие, происходящее на экране вызвало у них интерес.

Сотрудники кафедры поэтапно перематывали ролик и искали «вкравшуюся» ошибку, обмениваясь оживленными репликами: «Если решение строится на том, что это ромб, то оно неверно, поскольку две его вершины находятся на окружности», «А действительно ли эти хорды проходят через центр окружности? Видите, как дрогнула рука, когда она их чертила?».

И, хотя явной ошибки, подрывающей все математические устои, как и предупреждал Филипп Кораблёв, с ходу найти не удается, они остаются при своем мнении: решение не может быть правильным, потому что доказано обратное.

Рассказывая о невозможности решить задачу Архимеда, доцент Филипп Кораблев вспомнил, как в школе её предложила учительница математики, которая, видимо, просто устала от класса: «Мы пол-урока ломали головы и выдвигали свои версии, конечно, изначально неверные. И только после узнали, что она просто пошутила и водила нас за нос».

В 86 лет Ляля Гиззатовна Зарипова продолжает увлекать любимым предметом окружающих. К ней по-прежнему обращаются с просьбой подтянуть детей по математике. Отмечается, что после ее уроков ученик начинает стараться понять и решить, а не зазубрить или списать из интернета.

Одна из классических неразрешимых задач

Трисекция угла — задача о делении заданного угла на три равные части построением циркулем и линейкой. Иначе говоря, необходимо построить трисектрисы угла — лучи, делящие угол на три равные части.

Наряду с задачами о квадратуре круга и удвоении куба является одной из классических неразрешимых задач на построение, известных со времён Древней Греции.

Невозможность построения была доказана Ванцелем в 1837 году. Несмотря на это, в прессе и даже в некоторых научных журналах время от времени публикуются некоторые неверные способы осуществления трисекции угла циркулем и линейкой.