«Занимательное богословие». 7. Повесть о вечности
 - Хотя я и преподаю философию, - торжественно начал Назарий Валерьевич, - должен признать, что мой предмет далек от точности и непротиворечивости, без которых невозможна никакая серьезная наука. Христианское богословие в этом отношении куда больше соответствует критерию научности, поскольку разномыслия, расхождение в мнениях и прямые заблуждения, то есть ереси, всегда побеждались соборным опытом Церкви.
- Хотя я и преподаю философию, - торжественно начал Назарий Валерьевич, - должен признать, что мой предмет далек от точности и непротиворечивости, без которых невозможна никакая серьезная наука. Христианское богословие в этом отношении куда больше соответствует критерию научности, поскольку разномыслия, расхождение в мнениях и прямые заблуждения, то есть ереси, всегда побеждались соборным опытом Церкви.
Огромная заслуга святых отцов эпохи Вселенских соборов состоит в формировании основанных на философии неоплатоников языка и метода, которые позволили полно и непротиворечиво изложить богословское содержание Евангельского Откровения.
Сочинения Григория Богослова, Василия Великого, Григория Нисского, Максима Исповедника превратили православное богословие в строгую науку, способную точно и однозначно выразить самую сложную богословскую идею.
При этом золотой век византийской патристики, а по большому счету и вся история Церкви, – время весьма серьезной полемики на темы, так или иначе связанные с главным вопросом богословия – учением о спасении. Омиусиане и аномеи, афтардокеты и фтартолатры, имябожники и софиологи - все это лишь немногочисленные примеры отклонений от православного вероучения, которые возникают, главным образом, по причине терминологической неопределенности, которая присуща языку философии, используемому в богословии.
Идеалом точности до начала XX столетия считалась математика. Я сам до поступления на философский факультет три года обучался на мехмате. Поэтому вторжение этой науки в богословие всегда казалось мне неизбежным. Однако очень немногие богословы (Николай Кузанский, Флоренский) решались использовать математические образы в своем творчестве. Вероятно, такая робость была связана, во-первых, с трудностями в постижении самой математики, а с другой стороны, со страхом поверять бесконечность Божественного бытия конечной числовой мерой. И уж скорее математики (Лейбниц, Кантор), чем богословы, осмеливались начертать математические образы догматических построений.
Очевидно, что самой подходящей областью приложения математического метода в богословии могла бы стать та область догматики, в которой говорится о бесконечности: с одной стороны, бесконечности Божественного бытия, а с другой стороны, бесконечности Вечной Жизни, уготованной человеку после всеобщего Воскресения и Страшного суда.
Однако античная эстетика привнесла в европейскую науку и святоотеческое богословие страх перед актуальной бесконечностью. Бесконечность допускалась исключительно в потенциальном своем аспекте, как постепенное и последовательное вхождение в сферу Божественного бытия, как бесконечный асимптотический процесс феозиса, «становления по благодати тем, чем Бог является по природе» (Максим Исповедник).
Заметьте при этом, что бесконечности боялись, бесконечность могли считать неудобной мили непостижимой, но никто из великих мыслителей прошлого не считал ее скучной, как мой многоуважаемый оппонент.
Ориген и Аквинат наотрез отказывались признавать существование актуальной бесконечности на основании того, что Бог сотворил все «мерою, числом и весом» (Прем. 11, 21). При этом «число» понималось как конечная и определенная величина, а любая иррациональность понималась в духе античности как несовершенство и ущербность.
Даже в Своем бытии Бог не может быть бесконечным, так как бесконечность не имеет формы и не может быть мыслима. Правда, уже Блаженный Августин допускает, что Бог может мыслить все числа как одно целое, и представлять Бога конечным – значит ограничивать Его достоинство.
Открытия математики рубежа XIX и XX столетий показали, однако, что существуют иные трансфинитные числа, которые отражают разные уровни бесконечности. Оказалась, что сама математическая бесконечность – это не просто бесконечный пересчет конечных величин, а нечто качественно новое, целая иерархия, не имеющая предела в своем усложнении.
Теория множеств, созданная в это время немецким ученым Георгом Кантором, вместе с арифметикой кардинальных трансфинитных чисел может послужить наглядным и логически непротиворечивым образом Вечности, к которой предназначен и которую обретает человек после чаемого Всеобщего Воскресения.
2.
 |
| Философ Владимир Соловьев |
Философ Владимир Соловьев – все-таки я не могу совсем без философии – считал, что человеку присуще врожденное ощущение собственного бессмертия. По мнению великого русского мыслителя, феномен человеческой жизни определяется противоречием между знанием собственной смертности и верой в бесконечность своей жизни. Всякий человек неосознанно чувствует свою предназначенность к бессмертию, столь же инстинктивно протестует против неизбежности смерти, всеми силами пытается продлить жизнь за пределы своего физического существования.
Нет ничего удивительного в том, что любая религия (даже язычество, являющееся осколком истинного знания Бога) говорит о продолжении жизни человека после физической смерти. Удивительно то, что и вполне безрелигиозное сознание пытается преодолеть смерть. Бердяев, как известно, выводил творчество из феномена абсолютной свободы человека. Но с той же убедительностью можно сказать, что творчество вытекает из стремления продлить жизнь после смерти. Человек пытается сохранить свое личное присутствие в мире в плодах своего ума, своей души, своих рук. При этом самым простым, доступным и генетически достоверным способом продления своей жизни является ее продолжение в потомстве. Поэтому для неверующего в личное воскресение человека самая большая беда – бездетность. Ветхий Завет, союз Бога с Авраамом, основывается на обещании произвести из чресл престарелого праведника народ, многочисленный, как небесные звезды и морской песок. Потрясающая новизна христианства заключалась в учении о личном бессмертии, вере в грядущее воскресение всех умерших.
«Чаю воскресение мертвых и жизни будущаго века», - утверждает христианский символ веры. Завораживающее слово Вечность становится реальностью бесконечно длящейся жизни. Богослужебные тексты, употребляя слово смерть, как знак окончания земного существования, никогда не говорит об умерших, предпочитая называть тех, кто перешел границу земной жизни усопшими, ожидающими пробуждения. Сама Церковь осознает себя как Таинственное Тело Христово, заключающее в себе живых и тех, кого считает преставившимися, то есть «ПЕРЕставившимися», перешедшими от земного конечного существования к вечному бытию.
Вечность, которую проповедует христианство, вполне полноценна. Ни одна сущность, созданная Богом, не может быть уничтожена. Даже «Вторая смерть», уготованная в Апокалипсисе диаволу и «аггелам его», это не абсолютная деструкция, а только абсолютная изоляция, ввержение в «озеро огненное» (Откр. 20, 10, 14), то есть та же вечность.
Средневековое мировоззрение представляло эту вторую вечность, это «воскрешение осуждения» (Ин. 5, 29) весьма натуралистически. Геенна огненная, о которой говорил Христос, виделась чередой кипящих смоляных котлов и прочих вполне материальных ужасов, так что известный вольнодумец Федор Павлович Карамазов предполагал наличие в аду целой металлургии, для производства железных крючьев, которыми бесы истязают грешников. Святые отцы протестовали против такого натурализма, означавшего, по сути, увековечивание зла, бесконечную насмешку диавола над благим Промыслом Творца. Устраняя это противоречие, они находили сущность адских мучений то в бесконечной досаде за упущенную возможность обретения райского блаженства, то в угрызениях совести, невозможности раскаяться в содеянных грехах. В мучительных поисках сущности ада, в старании отыскать золотую середину между телесными и нравственными мучениями, богословы и философы постепенно начинали понимать, что дело вовсе не в характере мучений, а в их вечности.
Бог не играет с человеком. Даруя человеку Свой Образ, который заключается, прежде всего, в свободе воли, Господь предлагает ему избрать Жизнь или Смерть. Не принудительный рай, а достоинство свободы, возможность жить, исходя из побуждений собственного сердца, - вот в чем проявляется бесконечная любовь Бога к Своему самому совершенному творению. И вечный ад парадоксальным образом становится свидетельством Любви, кроме Которой в Боге нет никакого другого чувства. Позволяя человеку в границах земного существования быть свободным, разрешая ему губить себя, упорствовать во зле, отвергать спасение и само человеческое достоинство, жить по звериному, последовательно и сознательно наносить оскорбление своими грехами Любящему Отцу, Бог оставляет это право и в вечности.
Наказание вечностью оказывается страшным по разным причинам. Каждое мгновение вечности может оказаться наполненным максимальным мучением. Если спасение – это вечная жизнь, то «воскрешение суда» - это вечная смерть. К такому выводу приходит философ Евгений Николаевич Трубецкой, который в последней части своей книги «Смысл жизни», законченной в 1918 г., когда обломки разрушенной Россия все увереннее шли ко дну, высказал предположение, что сущность ада состоит в бесконечно длящемся и потому бесконечно мучительном умирании. В субъективном сознании грешника, мгновение смерти, отделение души от тела переживается как бесконечно продолжающееся, вечное переживаемое состояние.
Но еще более страшный образ ада устами одного из самых загадочных своих героев рисует Достоевский. Свидригайлов боится, что ад для него окажется чем–то до отвращения обыкновенным, вроде деревенской бани с пауками. Здесь нет смоляных котлов, раскаленных сковородок и пресловутых крючьев. Вечность оказывается страшна сама по себе, бесконечной повторяемостью одних и тех же до отвращения похожих, скудных, ущербных состояний. Такая вечность имеет в русской литературе еще одно яркое представление. В «Сценах из «Фауста» Пушкина герой, оказавшийся в преисподней, интересуется выигрышем у бесов, которые режутся в карты. Отрываясь на минуту от увлекательного занятия, один из бесов отвечает Фаусту:
Молчи! Ты глуп и молоденек,
Уж не тебе меня ловить.
Ведь мы играем не из денег,
А только б вечность проводить!
Назарий Валерьевич на минуту остановился, вытер пот со лба, осмотрелся вокруг. Парк Липки был пустынным как та самая вечность, о которой он только что повествовал.
Паузой не преминул воспользоваться Орленко.
- В русской литературе есть еще одно замечательное описание мучительности бесконечных повторений. Это стихотворение Владислава Ходасевича:
Нынче день такой забавный:
От возниц, что было сил,
Конь умчался своенравный,
Мальчик змей свой упустил,
Вор цыпленка утащил
У безносой Николавны…
Но попался вор нахальный,
Змей упал в соседний сад,
Мальчик ладит хвост мочальный,
И коня ведут назад.
Восстает мой тихий ад
В стройности первоначальной…
- Ну, да, - согласился философ, - восстает мой тихий ад в стройности первоначальной. Пожалуй, у Пушкина не так страшно. Там есть хотя бы игра, бессмысленная, бесконечная и бесплодная, мнимая, но все же деятельность, как у царя Сизифа… А Ходасевич все же писатель XX века. Здесь уже всеевропейские переживания… философия экзистенциализма, Сартр, «Тошнота»…
В повседневной жизни такая дурная бесконечность живо ощущается детьми. Открытие неограниченности натурального ряда, обнаружение отсутствия наибольшего числа вызывает, по меньшей мере, эмоциональное беспокойство. Бесконечная сказка о попе и его собаке, способная довести чувствительного ребенка до обморока – вот образ этой ужасающей вечности.
Заметим, что бесконечность может вызывать противоположные ощущения. Если Канта восхищала торжественная бесконечность звездного неба, то у Достоевского бесконечность вызывала отвращение и страх. Но может быть речь идет о разных бесконечностях, может быть между бесконечностью звездного неба и вечностью бани с пауками такая же пропасть, как между «воскрешением живота» и «воскрешением суда», о которых говорится в Евангелии от Иоанна (Ин. 5, 29)?
3.
 Образ Вечной жизни не менее проблематичен, чем образ «отрицательной вечности». «Не видел того глаз, не слышало ухо, и не приходило то на сердце человеку, что приготовил Бог любящим Его»(1 Кор. 2, 9). Эти слова апостола Павла являются свидетельством того, что тайны Небесного Царство непостижимы для не преображенного человеческого ума. Даже опыт святых может помочь здесь совсем немного. Сам Павел, восхищенный, по его же словам, «до третьего неба» (2 Кор. 12, 1-4), не мог найти слов для того, чтобы передать увиденное. Сочинения святых отцов, которых принято называть мистиками, - ПсевдоДионисия, Григория Богослова, Максима Исповедника, Симеона Нового Богослова понятны немногим. Их духовный опыт настолько превосходит знание обычного человека, что не находит адекватного выражения на общеупотребительном языке. Преподобный Серафим, объясняя собеседнику цель христианской жизни, вынужден показать результат стяжания Святого Духа, поскольку никаких слов для этого не хватает. Вечность Небесного Царства остается для нас закрытой.
Образ Вечной жизни не менее проблематичен, чем образ «отрицательной вечности». «Не видел того глаз, не слышало ухо, и не приходило то на сердце человеку, что приготовил Бог любящим Его»(1 Кор. 2, 9). Эти слова апостола Павла являются свидетельством того, что тайны Небесного Царство непостижимы для не преображенного человеческого ума. Даже опыт святых может помочь здесь совсем немного. Сам Павел, восхищенный, по его же словам, «до третьего неба» (2 Кор. 12, 1-4), не мог найти слов для того, чтобы передать увиденное. Сочинения святых отцов, которых принято называть мистиками, - ПсевдоДионисия, Григория Богослова, Максима Исповедника, Симеона Нового Богослова понятны немногим. Их духовный опыт настолько превосходит знание обычного человека, что не находит адекватного выражения на общеупотребительном языке. Преподобный Серафим, объясняя собеседнику цель христианской жизни, вынужден показать результат стяжания Святого Духа, поскольку никаких слов для этого не хватает. Вечность Небесного Царства остается для нас закрытой.
Блаженство жизни Будущего века, отблеск которого немногие святые видели уже в жизни земной, является предметом веры. Но и вера требует какого-то зримого образа, какого-то понятного представления. Конечно, христианство не признает чувственного рая ислама. Но в простонародном средневековом представлении Царство Небесное оказывалось наполненным тем, чего простому человеку так не хватало в земной жизни. Рай представлялся местом отдохновения от тяжких трудов, обителью, «идеже несть болезнь, ни печаль, ни воздыхание».
Это вполне апофатическое описание оставляет много вопросов о сущности райского блаженства. Не обратится ли вожделенный покой в бесконечную праздность с неизбежной бесконечной скукой? Не будет ли вечность рая унылой бесконечностью натурального ряда чисел, в котором за числом N с железной предопределенностью следует N+1 ?
Уверенность в том, что рай – это не полчища ангелов с арфами, придает внимательное чтение Священного Писания. О том, что Вечность Небесного не является бесконечно длящимся временем, свидетельствует Ангел Апокалипсиса, который «клялся Живущим во веки веков, Который сотворил небо и все, что на нем, землю и все, что на ней, и море и все, что в нем, что времени уже не будет» (Откр.10,6). Понимаете, времени в Царстве Небесном не будет. То есть блаженная вечность не является бесконечно длящимся временем. Это нечто иное. Что же?
Задумываясь о «жизни Будущего века», апостол Павел говорит о том, что в Царстве Небесном многое откроется: «Ибо мы отчасти знаем, и отчасти пророчествуем. Когда же настанет совершенное, тогда то, что отчасти, прекратится….Теперь мы видим как бы сквозь тусклое стекло, гадательно, тогда же лицем к лицу; теперь знаю я отчасти, а тогда познаю, подобно, как я познан» (1 Кор.13: 9 - 12).
Ценность будущей жизни, ее радость и блаженство, таким образом, заключаются в познании того, что в земной жизни видится тускло и гадательно. Безусловно, это -Божественная Истина и само Божественное Бытие. Отсюда проистекает мнение некоторых из святых отцов, согласно которому в Блаженной Вечности спасенный человек будет испытывать бесконечную радость от бесконечно длящегося познания бесконечного Творца. Об этом говорит Своим ученикам Сам Господь Иисус Христос: «Сия же есть жизнь вечная, да знают Тебя, единого истинного Бога, и посланного Тобою Иисуса Христа» (Ин.17,3). Действительно, Бог бесконечен в Своем Существе и в Своих Свойствах. Познание такого объекта требует бесконечного усовершенствования познающего, его вхождения в бесконечность, превышающую время.
И это познание - не унылый перебор однообразных комбинаций, характерный для любой игры от шахмат до преферанса, это - бесконечное восхождение от одного уровня бытия к иному, наполненному принципиально новым содержанием.
А вот теперь, самое интересное… Жаль, что в Липках нет доски… Ну ладно, если понадобится, начертим вон в той песочнице…
Поддержку святоотеческого мнения о характере Блаженной Вечности оказывает математика, которая подтверждает, что вечность – это не просто бесконечно длящееся время, а новое качество человеческого существования.
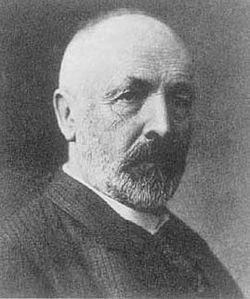 |
| Математик Георг Кантор |
Речь идет о теории трансфинитных чисел Г. Кантора. Первая бесконечность, с которой человек встречается в жизни, - это бесконечность счета: один, два, три…, которую математики называют натуральным рядом. В повседневности мы легко обходимся этими натуральными числами, и только тот, кому приходится заниматься дележкой, обращается к обыкновенным или десятичным дробям. Оказывается, что всевозможных обыкновенных дробей (математики называют такие дроби рациональными числами) ровно столько же, сколько натуральных чисел. Рациональные числа можно пересчитать. Поэтому это множество, так же как любое другое, элементы которого можно поставить во взаимно-однозначное соответствие с натуральными числами, называют счетным…
Здесь вся компания вслед за преподавателем перешла к песочнице, где выпускник мехмата попытался изобразить незамысловатый способ, каким Кантор установил взаимно-однозначного соответствия множества натуральных и множества рациональных чисел.
Редкие прохожие, видимо, воспринимали нарисованные вавилоны как некие каббалистические знаки, а саму группу не иначе как тайную масонскую ложу на выездном заседании.
Нарисованную на песке схему, кажется, понял один Дима Полохов, настолько же умный, насколько осторожный студент, закончивший перед поступлением в семинарию физический факультет университета. Всем остальным оставалось только поверить, что такое соответствие существует. Философ увлеченно продолжал:
- Эту первую встреченную человеком бесконечность, не только умопостигаемую, но и непосредственно наблюдаемую, вполне можно считать математической характеристикой земной жизни, которая, как известно, далека от совершенства. Точно также, бесконечный натуральный ряд можно считать и образом бесконечно длящегося и бесконечно дробимого времени. При этом каждый новый момент ничем принципиально не отличается от предыдущего.
Выпускники общеобразовательных школ знают, что существуют еще какие-то иррациональные числа, наводившие тоску еще на древних греков, числа, которые могут быть записаны только в идее бесконечных непериодических дробей. Школьник сможет назвать два – три таких числа: пи, е, квадратный корень из двух… В действительности, оказывается, что этих иррациональных чисел гораздо больше, чем рациональных.
- Нематематику трудно понять, как это одна бесконечность может оказаться больше другой бесконечности. Однако даже нематематик без труда поймет найденное Кантором доказательство того, что «бесконечность» (в теории множеств – мощность) ряда натуральных чисел меньше «бесконечности» (мощности) вещественных (рациональных + иррациональных) чисел[1].
Ну, насчет того, что «может понять даже нематематик», философ несколько загнул. Дальше не понимал уже и Полохов… Однако напор мысли Назария Валерьевича был наполнен такой жизненной силой, что на отсутствие строгого доказательства никто не обращал внимания. Все ждали развязки… И она наступила!
- При этом, - продолжал философ, - мощность вещественных чисел (континуума) вполне можно считать аналогом вечности, взятой в богословском аспекте. О том, что это действительно новое качество существования говорит тот простой факт, что мощность множества вещественных чисел совпадает с мощностью ограниченного подмножества, например, отрезка числовой оси от нуля до единицы[2]. Понятно, что такой отрезок может быть сколь угодно малым. В богословском аспекте интервал (0,1) – это аналог Образа Бесконечного Бога в ограниченном человеке. Если он равномощен целому, то и человек способен к бесконечному познанию!
 Интуиция такого рода запечатлена в одном замечательном четверостишии Уильяма Блейка, которое в пресноватом переводе Маршака звучит примерно так:
Интуиция такого рода запечатлена в одном замечательном четверостишии Уильяма Блейка, которое в пресноватом переводе Маршака звучит примерно так:
В одном мгновенье видеть вечность,
Огромный мир - в зерне песка,
В единой точке – бесконечность
И небо в чашечке цветка…
Но самое интересное заключается в следующем. Кантор (размышляя, кстати, о догмате Пресвятой Троицы) построил целую арифметику трансфинитных чисел.
Первое трансфинитное число алеф ноль было мощностью натурального ряда. Следующее алеф 1 получалось как 2 в степени алеф 1 и так далее. Хотя эта арифметика непротиворечива, некоторые математики относятся к ней с недоверием, поскольку не найдено и не сконструировано ни одного множества, мощность которого была бы равна алеф 2, алеф 3, и т.д. Алеф 1 в определенной аксиоматической системе совпадает с мощностью континуума. Другими словами в земном существовании нет объектов (включая мыслимые математические структуры !) «уровень бесконечности» которых
превышал бы бесконечность действительных чисел[3]. Но поскольку теория трансфинитных чисел все же является реальностью, она может навести на мысль, что существуют идеальные структуры, имеющие уровень выше бесконечности континуума, которая не может быть превышена в обычном мире.
Это и есть образ той Вечности, которая ожидает человека в Царстве Небесном. Понятно, что постижение такой вечности, с возможным переходом от одного уровня познания к другому в соответствии с арифметикой Кантора, является бесконечным процессом духовного преображения человека, удостоенного спасения. И это, безусловно, более интересное и деятельное существование, чем однообразное проживание длительности натурального ряда.
Назарий Валерьевич остановился. Чувствовалось, что он нисколько не жалеет о потерянном уроке. Он высказался и изложил перед студентами теорию, которая, возможно, сложилась у него еще во время обучения в университете. Студенты молчали. С одной стороны, непривычная для них математика да еще в применении к богословию не очень то проясняла суть вопроса. А кроме того, и сама проблема была для них не очень злободневной. По молодости лет, мало кто задумывался о том, чем же будет заполнена блаженная вечность, до которой еще предстояло добраться через целую жизнь, обещавшую быть и радостной, и искусительной.
- Ну, как? Теперь понятно, что такое вечность? - философ с робостью смотрел на притихших семинаристов.
- Темна вода во облацех небесных, - перекрестился Орленко.
- Отчего же темна? - возразил Прибыткин, которому хотелось подбодрить преподавателя, в пылу увлечения высказавшего самые сокровенные мысли. Правда, к этому простому чувству примешивалось желание самому быть на высоте обсуждаемой проблемы и, самое главное, столь мудреного метода. - Отчего же темна? Все очень даже понятно. Это как у Фихте «Ясное, как солнце, сообщение широкой публике о подлинной сущности новейшей философии». Или «О подлинной сущности вечности». А вообще, знаете, как говорил один протодьякон? Премудрость бросьте! Будьте просты как голуби! Мы, может быть, и не очень образованные люди, но мы же верующие христиане. Как писал апостол Павел, «знание надмевает, а любовь назидает» (1 Кор. 8, 1). Будем просто верить, что Господь уготовал каждому верующему человеку блаженную вечность. А уж в чем она заключается? А вот как помрем, так и узнаем. Можно же немного потерпеть… Как говорит отец инспектор: пораньше умрешь, поменьше нагрешишь… А пока будем верить нашему православному Символу веры: «Чаю воскресения мертвых и жизни будущего века!».
- Аминь! - несвойственным басом пропел Орленко. - Спаси Христос, Назарий Валерьевич, за лекцию. Простите, если мы чего-то не поняли. Но мы будем просто верить, что Господь в вечности никого не обидит, и она, эта вечность, не окажется невыносимо скучной. Ведь верить легче, чем знать.
- Ты знаешь, для меня, честно говоря, знать легче, чем верить, - признался философ, все еще не успокоившийся после своего бурного монолога.
- Да вы, Назарий Валерьевич, просто какой-то осколок Серебряного века. Для них тоже было легче знать, чем верить… Владимир Соловьев, Бердяев, отец Павел Флоренский…Вот уж где премудрость! - снова подал голос Прибыткин. - Но вот знаю я одного архимандрита, который говорил: если бы у меня был пистолет, то моя рука тянулась бы к нему всякий раз, когда я слышу имена Соловьева, Флоренского, Булгакова, Бердяева и иже с ними…
- Так то оно так, Сережа. Но ведь тот же отец Павел Флоренский подтвердил подлинность и силу своей веры - именно веры, а не отвлеченного знания - мужественным поведением в годы советской власти. И даже мученической смертью! Да и наши эмигранты вели себя за границей очень достойно. Тот же Бердяев, тот же отец Сергий Булгаков…Кому-то верить легче, чем знать. Кому-то наоборот. Одно только следует помнить: верить – всегда радостно, а вот знать – далеко не всегда! Вспомни Екклезиаста: «во многой мудрости много печали; и кто умножает познания, умножает скорбь» (Еккл. 1,18). Ладно, чтобы не умножать скорбь, урок закончен! Да и обедать пора…
Идти на обед было совсем недалеко. Здание семинарии располагалось в двух шагах от Липок, где проходили наши богословские собеседования. Аллея, покинутая студентами как-то очень быстро заполнилась людьми, будто они стояли где-то в ожидании, чтобы не помешать разговору, и теперь все разом с детскими колясками, собаками на поводках, газетами, мороженым, бутылками с пивом, - высыпали на освободившееся пространство.
Последним из парка уходил философ. Он был задумчив и медленно повторял:
- Надо же, премудрость бросьте!… Да как же ее бросишь, когда сложное понятнее простого…
[1] Кантор начал своё доказательство с предположения, что существует взаимно однозначное соответствие между множеством действительных чисел и множеством целых чисел. Последующим рассуждением показывается, что это предположение приводит к противоречию, отсюда следует, что первоначальное предположение неверно и такое взаимно однозначное соответствие невозможно. Рассуждение можно упростить, рассматривая только множество действительных чисел, заключённых между 0 и 1. Если это множество больше множества целых чисел, то множество всех действительных чисел и подавно больше него. Итак, предположим, что действительные числа, заключенные между 0 и 1, могут быть одно за другим объединены в пары с целыми числами. Установление такого соответствия эквивалентно составлению некоторого перечня действительных чисел, каждое из которых представляется как бесконечная десятичная дробь. Но оказывается, что можно определить новое действительное число, не включённое в этот перечень. Для того, чтобы показать это, берём первую цифру первого десятичного разложения в указанном перечне действительных чисел. Если эта цифра равна 1, то пишем 9 на первом месте после запятой. Если первая цифра в этом перечне не равна 1, то на первом месте определяемого числа пишем 1. Построение нашего нового числа продолжается затем путём изменения второй цифры второго десятичного разложения в перечне, третьей цифры в третьем десятичном разложении и так далее. Вновь построенное число должно отличаться по крайней мере одним десятичным знаком от каждого действительного числа, содержащегося в перечне, однако оно тем не менее представляет собой некоторое действительное число, расположенное между 0 и 1. Поэтому можно построить некоторое число, не содержащееся в перечне действительных чисел, и таким образом предположение, что все действительные числа можно пересчитать, приводит к противоречию.
[2] Это верно и для множества рациональных чисел.
[3] Может показаться, что мощность множества комплексных чисел превышает континуум. Однако сам Кантор доказал, что мощность множества точек квадрата совпадает с мощностью интервала (0,1), то есть плоскость эквивалентна прямой.
Читайте также:
По следам Перельмана, или «Занимательное богословие»
«Занимательное богословие». 1. Почему я лучше всех?
«Занимательное богословие». 2. О соборности, авторитете и блудобесной американской резине
«Занимательное богословие». 3. Безобидно ли язычество?
«Занимательное богословие». 4. Наши экскурсоводы
«Занимательное богословие». 5. Если Бог есть, то все позволено…
Занимательное богословие. 6. Нищий – это звучит гордо















1. «Что было раньше: яйцо или курица?»
Даются два понятия «ЯЙЦО» и «КУРИЦА» и в РЯДУ ПОСЛЕДОВАТЕЛЬНО РАЗВЁРТЫВАЕМЫХ ПОНЯТИЙ (РПРП) требуется найти понятия предшествующие к каждому из них.
В РПРП для "ЯЙЦА" предшествующим является "КУРИЦА", ибо понятием «эмбрион» (или другими ) не интересующим нас по постановке вопроса мы можем пренебречь.
В РПРП для "КУРИЦА" пренебрегаемым понятием является «цыплёнок», но не «треснувшееся яйцо (из которого старается вылупиться цыплёнок)», ведь в постановке вопроса не акцентировано внимание на обязательности рассмотрения лишь яйца целостного состояния, т. е. для "КУРИЦА" предшествующим является не то понятие на котором акцентирован вопрос, а его разновидность.
ВЫВОД: "КУРИЦА"
2. Даётся понятие "Недвижущегося (Ахиллес)" , который не состоит в РПРП и отсутствие динамического состояния у которого завуалировано перемещениями, которую следуя Зенону производим и мы переставляя это понятие на предыдущие позиции в РПРП понятия "Движущегося (черепаха)" - вот в этом и вся загадка этого апория Зенона. В такой постановке вопроса даже Усейну Болта не тягаться с черепахой...